Deadlock in Operating System Tutorial Notes Study Material with Example

Deadlock

In a multiprogramming environment, a situation when permanent blocking of a set of processes that either compete for system resources or of communication with each other happens, we can call this as deadlock situation. This deadlock problem involves conflicting needs for resources

By two or more processes.

Necessary Conditions for Deadlock

A deadlock situation can arise, if the following four conditions hold simultaneously in a system.

Mutual Exclusion

Resources must be allocated to processes at any time in an exclusive manner and not on a shared basis for a deadlock to be possible. If another process requests that resource, the requesting process must be delayed until the resource has been released.

Hold and Wait Condition

Even if a process holds certain resources at any moment, it should be possible for it to request for new ones. It should not give up (release) the already held resources to be able to request for new ones. If it is not true, a deadlock can never take place.

No Preemption Condition

Resources can’t be preempted. A resource can be released only voluntarily by the process holding it, after that process has completed its task.

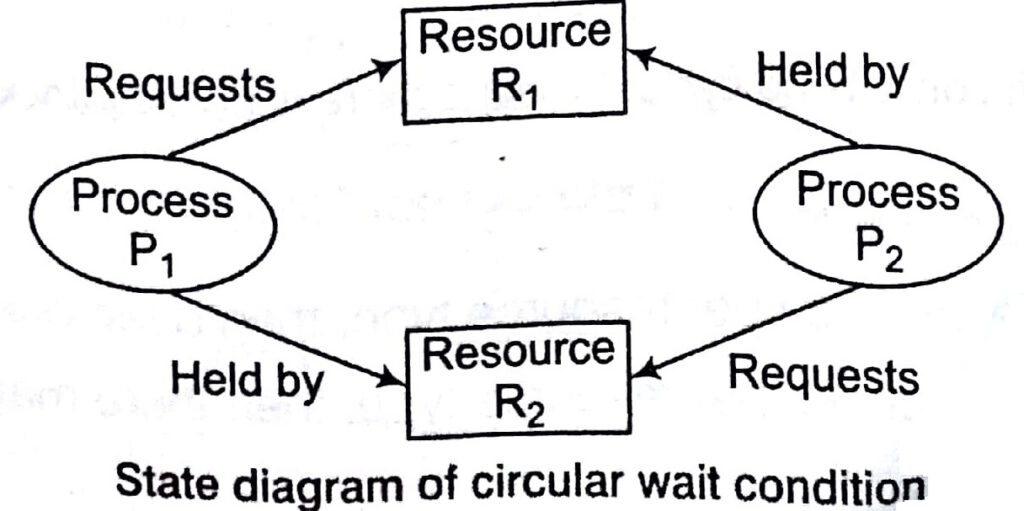
Circular Wait Condition

There must exist a set = {Po^, Pi^, P2, …, ^Pn^} of waiting processes such that P_o is waiting for a resource that is held by PI, P1

_weld_. by                                                                                                              is waiting for a resource that is

P_r, _ ₁ is waiting for a resource that is held by P_r, and P_n is

Waiting for a resource that is held by Po.

Resource Allocation Graph

The resource allocation graph consists of a set of vertices V and a Set of edges E.

vertices V is partitioned into two types

• P = {P₁, P₂,…, P_n}, the set consisting of all the process_{es in t}
• R = {R₁, R₂,…, R_m}, the set consisting of all resource typ_es in 1f,.
• Directed Edge P       R_i is known as request edge.
• Directed Edge R ;      P is known as assignment edge.

 Resource Instance

• One instance of resource type R₁. Two instances of resource type R₂.
• One instance of resource type • Three instances of resource type R₄.

R2

Example of resource allocation graph

Process States 

• Process P₁ is holding an instance of resource type R2 and is waiting for an instance of resource type R₁.
• Process R₂ is holding an instance of R₁ and R2 is waiting for an instance of resource type
• Process P₃ is holding an instance of R₃.
• Basic facts related to resource allocation graphs are given below

Note: If graph consists no cycle it means there is no deadlock in the system

If graph contains cycle

• If only one instance per resource type,
• If several instances per resource type,

Deadlock Handling Strategies

1. Deadlock prevention    2. Deadlock avoidance   3.Deadlock detection

Deadlock Prevention

Deadlock prevention is a set of methods for ensuring that at least one of the necessary conditions can’t hold.

Deadlock Avoidance

A deadlock avoidance algorithm dynamically examines the resource allocation state to ensure that a circular wait condition can never exist The resource allocation state is defined by the number of available and allocated resources and the maximum demands of the processes.

Safe State

A state is safe, if the system can allocate resources to each process and still avoid a deadlock.

A system is in safe state, if there exists a safe sequence of all processes. A deadlock state is an unsafe state. Not all unsafe states cause deadlocks.

Banker’s Algorithm

Data structures for Banker’s algorithm available. Vector of length m. If available [j] = k, there are k instances of resource type R₁ available.

• Max n x m If max [i, j] = k, then process P_i may request at most k

instances of resource type R_j.

• Allocation n x m If allocation [i, j ] = k, then P_i is currently allocated k instances of R_i
• Need n x m matt^-. If need [i, j I = k, then P_i may need k more instances of R to complete its task

Need [i,j]= max [i, j] — allocation [i, j]

.

• safety Algorithm

Step 1:  Let work and finish be vectors of length m and n, respectively. Initialize.

Work = Available

Finish [i]= False (for i=1,2,….n

 

Step ₂ :  Find i such that both

• Finish [i]. False
• Need ≤ Work

If no such i exists, go to step 4. Step 3 Work = Work + Allocation

Finish [i]= Tree            .

Go to step 2.

Step 4:  Finish [I] = True (for all i)

Then, the system is in a safe system. Example Banker’s Algorithm

 

As available resources are (3 3 2). The process P₁ with need (^{1 2} be executed.

Available resource = Available + Allocated resource of P_I

3 3 2

2 0 0

5 3 2

N_ow, available resources are (5 3 2).

The next process that can be executed after assigning available resource is P3. Thus, P₃ will execute next.

N_ow, available resource = Available resource + Resource of P₃

5 3 2

2   1 1

7  4  3

Now, available resources are 7 4 3. Next process will be P4.

A B C

7 4 3

0 0 2

7 4 5

Next process that will be executed is P_o.

Available resource

7  4  5

0  1  0

7  5  5

Key Points

• The sequence < P, P₃, P₄ P₀ P2 > ensures that the deadlock will never occur.
• If a safe sequence can be found that means the processes can run concurrently and will never cause a deadlock.
• First in first out scheduling based on queuing.
• Shortest seek time scheduling is designed for maximum through put in most scenarios
• RR scheduling involves extensive overhead, especially with a small time unit. Kernel is defined as a program running all times on the computer. It is the part of operating system that loads first. In simple word, kernel provides the communication between system software and hardware.

Deadlock Detection

Allow system to enter deadlock state and then there is

(i) Detection algorithm                                      (ii) Recovery scheme

Single instance of each resource type

• Maintain wait for graph.

(a) Nodes are processes.                              (b) P–> P_i, if P_i is waiting for P_i.

• Periodically invoke an algorithm that searches for a cycle in the graph.
• An algorithm to detect a cycle in a graph requires an order of n² operations, where n is the number of vertices in the graph.

 

Recovery Scheme

• Resource preemption
• Process termination
• Abort all deadlock processes
• Abort one process at a time until the deadlock cycle eliminated

---

Sorting in Design and Analysis of Algorithm Study Notes with Example

Learn Sorting in Handbook Series:  Click here 

Follow Us on Social Platforms to get Updated : twiter,  facebook, Google Plus