Number System in Switching Theory and Computer Architecture Notes
Switching Theory And Computer Architecture
Number System
This basically means the presentation of number with limited number of symbols. The decimal number system is said to be of base or radix 10 because it uses ten digits (0-9) to represent any number.
To distinguish between numbers of different bases, we enclose the value in parenthesis and with a subscript equal to the base is used.
e.g., If 10 is a decimal value, then (10)10
If 10 is a binary value, then (10)2

So, a number system with radix r will have r symbols and any number will be Interpreted as
anrn + an-1 rn-1 +……+ a0r0

Key Points
- The symbols (an, an_1, …, a0) should be one of the r symbols allowed in number system (i.e., from 0 toIn this, a,, is called as most significant digit and a0 is called the least significant digit.
Number Base Conversions
Decimal to Binary
We can understand this with the help of an example, converting decimal 31 to binary.
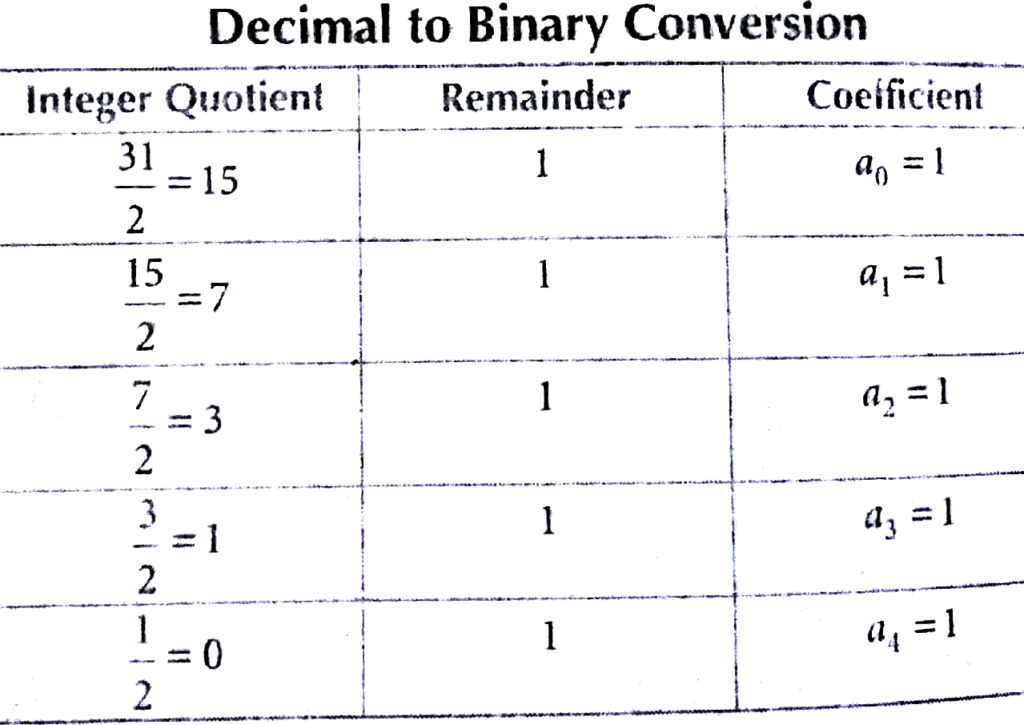
The binary number will be written as (a4 a3 a2 al a0)2 i.e., (11111)2.
Process
The given number should be divided by 2 to give an integer quotient and a remainder. The quotient is again divided by 2 to give a new quotient and remainder. The process is continued, until the integer quotient becomes 0. The coefficient of the desired binary number are obtained form the remainder as shown in the table.
e•g,, For fractional part
Convert (01 245)10 to binary upto 6 bits.
Process
First (0.1245)10 is multiplied by 2 to give an integer and a fraction. The new fraction is multiplied by 2 to give a new integer and a new fraction. This process is continued until the fraction becomes 0 or until the number of digits has sufficient accuracy. The coefficient of binary number are obtained from the integers as shown in the table.
Coefficient of Binary Number
| Fraction x 2 | Fraction | Integer | Coefficient |
| 0.1245 x 2 = 0.249 | 0.249 | 0 | a_1 =0 |
| 0.249 x 2 = 0.498 | 0.498 | 0 | a_2 = 0 |
| 0.498 x 2 = 0.996 | 0.996 | 0 | a_3 = 0 |
| 0.996 x 2 =1992 | 0.992 | 1 | a_4 =1 |
| 0.992 x 2 =L984 | 0.984 | 1 | a_5 =1 |
| 0.984 x 2 =1.968 | 0.968 | 1 | ‘ a-6 = I |
Thus, (0.1245)10 = (0.000111)2
i.e., (a_1 a_2 a_4 a_8 a_5)2
Decimal to Octal Conversion
We follow the same procedure as in case of decimal to binary except the base is changed now i.e., instead of 2 it is 8 now. So, wherever we have used 2 for multiplication or for division (in case of decimal to binary) we will use 8 in case of octal conversion.
e.g., (41)10 = (51)8
Decimal to Octal Conversion

Binary to Octal or Hexadecimal Conversion
Since, 23 = 8 and 24 = 16, each octal digit corresponds to three binary
digits and each hexadecimal digit corresponds to four binary digits. The conversion from binary to octal is easily accomplished by partitioning the binary numbers into group of 3 digits each as given below.

Conversion, from binary to hexadecimal is similar, except the binary number is divided into group of 4 digits.
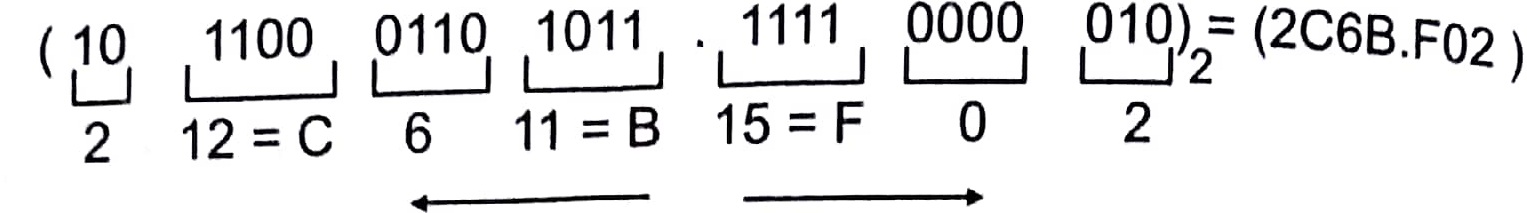
Key Points
- Partitioning is done from right to left for integer part and from left to right for fractional part.

Octal to Decimal Conversion
The same technique is applied over here as applied in case of binary to decimal except here our radix is 8, so we use powers of 8.
Complements
Complements are used in digital computer system for simplifying the subtraction operation and for logical manipulation.
There are two types of complements for each base r system,
- The r’ s complement 2. The (r — 1)’s complement
The r’s Complement
Given a positive number N with base r with an integer part of n digits. The r’s complement of N is defined as rn — N for N 0 and 0 for N = 0.
e.g., 10’s complement of (25.639)10 is (102 — 25.639)
100 — 25.639 = 74 — 361, here the number of digits in integer part is 2 means n = 2.
The (r -1)’s Complement
Given, a Positive number N in base r with an integer part of n digits and a fraction part of m digits, the (r — 1)’ s complement of N is defined as — N. rn-r-m-N
-
l’s complement of (52520)10 is (105 —1— 52520)
= 99999 — 52520 = 47479
Because number of integer part is 5, so rn =105 and no fractional part is present’ so r-rn = 10-0 =1
-
l’s complement of (0.3267)10 is (10° —10-4 — 0.3267)
=1— 0.0001— 0.3267
= 0.9999 — 0.3267 = 0.6732
No integer part, so 10n = 1 0° =1
-
complement of (101100)2 is (26 — 2-°)10 — (101100)2
= (64 — 1)10 — (101100)2
= (63)10 = (101100)2
= 111111— 101100 = 010011
Key Points
520 –>4 Here, n = 3, but (052) –>here n = 2.
- In the later example 0 is of no significance.
*In this cyberpointsolution.com we are trying to explain each and every concept of Number System in Switching Theory and Computer Architecture Notes
Alternative Conversion Process
For l’s Complement
Replace 0’s by l’s and l’s by 0’s.
e.g., 1’s complement of (1 0 0 1 1 0)2 = (011001)2
↓ ↓ ↓ ↓ ↓ ↓
0 1 1 0 0 1
For 2’s Complement
To start at the Least Significant Bit (LSB) and copy all the zeroes (Working from LSB towards the most significant bit) until the first 1 is reached, then copy that 1 and take complement all the remaining bits.
e.g., 2’s complement of

Properties of 2’s Complement
2’s complement representation allows the use of binary arithmetic operations on signed integers, yielding the current 2’s complement result.
2’s Complement of Positive and Negative Number
- Positive Numbers Positive 2’s complement numbers are represented as the simple
- Negative Numbers Negative 2’s complement numbers are represented as the binary number that when added to a positive number of the same magnitude equals zero.
Key Points
- The most significant (left most) bit indicates the sign of the integer, therefore, it is sometimes called the sign bit. If the sign bit is zero, then the number is greater than or equal to zero or positive.
- If the sign bit is one, then the number is less than zero or negative.
Subtraction Using l’s Complement
e.g., (19 — 3) = ?
(19)10 = (0001 0011)2
(3)10 = (0000 0011)2
Now we take l’s complement of 3 i.e., (1111 1100)2
Now, we add binary equivalent of 19 and l’s complement of 3.
0001 0011
+1111 1100
this is Carry bit 1 0000 1111
1
(00010000)2= (16)10
we need to add carry bit in case of l’s complement method.
e.g. , (3 —19; =?
(3)10 = (0000 0011)2
(19)10= (0001 0011)2
Now: we take 1’s complement of 19 i.e., (1110 1100)2
Now, we add binary, equivalent of 3 and l’s complement of 19.
0000 0011-4 Binary equivalent of 19
1100 2′ s complement of 3
1110 1111
Here, we don’t find any carry bit, so in this case we need to take complement of the sum and put a negative sign with it. This will be our final answer.
(1110 1111)2 -4 l’s complement is (0001 0000)2 = (16)10
we should a negative sign so —16 is our answer.
Subtraction Using 2’s Complement
e.g., (19— 3) =?
(19)10 = (0001 0011)2
and (3)10 = (0000 0011)2
2’s complement of 3 = (1111 1101)2
Add binary equivalent of 19 and 2’s complement of 3
0001 0011 –>Binary equivalent of 19
+ 1111 1101 –>4 2′ s complement of 3
10010000
So, result is (00010000)2 = (16)10
e.g, (3=19)=?

Since, no carry bit is there, we need to take 2’s complement of the sum. This will be our final result with a negative sign.
2’s complement of (11110000) = (0001 0000)2 = (16)10 So, result will be —16.
Example of 2’s Complement
Find out (— 3 —19) using 2’s complement. This is an special case. Here, we need to add 2’s complement of 3 and 2’s complement of 19.
1111 1101 –> 2’s complement of 3
This 1 is carry but 1 +1110 1101 2′s complement of 19
1110 1010
Drop the carry and take the 2’s complement of result because here both the numbers are negative. So, the result will be 2’s complement of (1110 1010)2 i.e., (0001 0110)2 = (22)10, additionally we need to put a — (minus) sign with the result , i.e., — 22. This will be our final result.
Sorting in Design and Analysis of Algorithm Study Notes with Example
Follow Us On Cyber Point Solution Youtube Channel : Click Here
Follow Us on Social Platforms to get Updated : twiter, facebook, Google Plus
Learn More Ethical Hacking and Cyber Security click on this link. cyber security
