Importance and Rules of Boolean Algebra Tutorial with Examples

Boolean Algebra

Boolean algebra is an algebraic structure defined on a set of elements together with two binary operators (+) and (.)

Closure

For and y in the alphabet A, x + y and x. y are also in A.

Duality

If an expression  contains only the operations AND, OR and NOT. Then, the dual _iof that expression is obtained by replacing each AND by OR, each OR by AND, all occurrences of 1 by 0 and all occurrences of 0 by 1.

Key Points

Principle of duality is useful in determining the complement of a function.

Boolean Operators

There are four Boolean operators

1. AND (•) operator (A .B)                2. OR (+) operator (A + B)
2. NOT (A / A’) operator
3. XOR (q operator (A+B=A-B+A•B)

Operator Precedence

The operator for evaluating Boolean expression is

1. Paranthesis                      2. AND                          3. NOT                              4. OR.

Boolean Function

• A Boolean function is an expression formed with binary variables, the binary operators (+, .), the unary operator (—), parenthesis and equal sign.
• For a given value of variable, the function can take only one value either 0 or 1.
• A Boolean function can be shown by a truth table. To show a function in a truth table we need a list of the 2^“ combinations of ‘s and O’s of the n binary variables and a column showing the combinations for which the function is equal to 1 or 0. So, the table will have 2^“ rows and columns for each input variable and the final output.

Canonical and Standard Form

• A canonical form is a unique representation for a given symbolic 1pression. If two expressions have the same canonical form, they must _represent the same function.
• Boolean functions expressed as a sum of minterms i.e.. sum of products.
• A minterm is a special product of literals in which each input variable appears exactly once. Function with n variable has 2ⁿ
• A maxterm is represented as sum of variable. n variables can be combined to form 2ⁿ Each maxterm is obtained from OR of the nvariab►es, with each variable being unprimed, if the corresponding bit of the binary number is 0 and primed, if the binary number is 1.

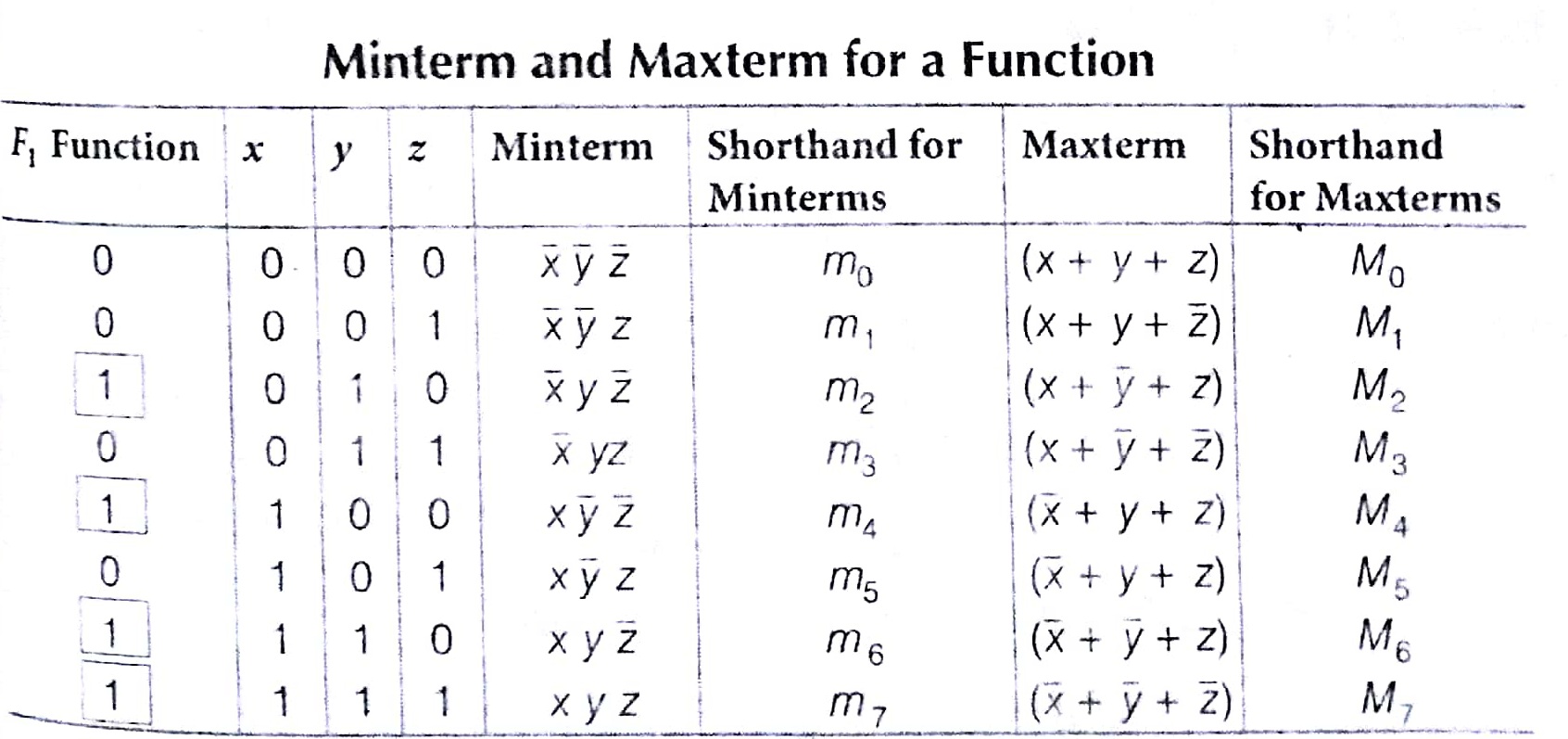
Wherever value of function F₁ is 1, corresponding minterm will be considered.

Key Points

• Two functions of n binary variables are said to be equal, if they have same value for all possible 2′ combinations of the n variables.

• 

• In this cyberpointsolution.com we are trying to explain each and every concept of Importance and Rules of Boolean Algebra Tutorial with Examples
  

Representation of Boolean Function

Using Minterm

A Boolean function may be expressed algebraically form given truth table by ^forming a minterm for each combination of the variable which produces a ¹ In the function and taking the OR of all those terms. We can refer the Preceding table.

Thus, function F₁ will be written as

F1 = xyz + xyz + xyz + xyz

Here, we have selected only those minterms for which

F₁ = 1 and F₁ will be represented (using minterm)

F₁ = Ʃ (2, 4, 6, 7) = Z(m₂, m₄, m₆, m₇)

As, F₁ = 1 for 010, 100, 110 and 111 those decimal equivalents are 2, 4, 6 and 7, respectively.

Representation of Boolean Function using Maxterm

For maxterm representation use those maxterms for which F₁ = 0 i.e., which produce 0 in the function. Then, form the AND of all those maxterm.

Thus, f_l will be given by the below Boolean expression

= (x + y + z). (x + y+ z). (x +y +z). (x + y + z)

= M_o M₁ M₃ M₅

F₁ will be represented as

= П(0, 1, 3, 5)

---

Sorting in Design and Analysis of Algorithm Study Notes with Example

Follow Us On Cyber Point Solution Youtube Channel : Click Here

Follow Us on Social Platforms to get Updated : twiter,  facebook, Google Plus

Learn More Ethical Hacking and Cyber Security click on this link. cyber security