Graph in C Language Tutorial Notes Study Material with Examples

Graph

A graph is a set of vertices and edges which connects them. A graph G consists of two things

1. A set of vertices V.
2. A set of edges E such that edge e in E is identified with a unique pair u, v of vertices in V, denoted bye = {u, v}

• Path: A path P of length n from a node u to a node v is defined as a sequence of (n + 1) nodes.

   P = (v₀, v ₁,  v₂ ,…, v _n)

• Adjacent Nodes or Neighbours: Suppose e [u, vi then the nodes u and v are called the endpoints of e and u and v are said to be adjacent nodes or neighbours.
• Degree of a Node: The number of edges containing u, is the degree of a node deg (u). If deg(u) = 0, this means u doesn’t belong to any edge, then u is called as isolated node.
• Connected Graph: A graph G is said to be connected, if there is a path between any two of its nodes.
• Complete Graph: A graph G is said to be complete, if every node u in G is adjacent to every other node v in {Number of edges with n nodes in a complete graph G

                                               =n (n —1)/2

• Tree Graph or Free Tree/Tree A connected graph T without any cycles is known as tree graph or free tree or simply a tree.

If T is a finite tree with k nodes, then T will have (k —1) edges.

Labelled and Weighted Graph

A graph G is said to be labelled, if its edges are assigned data. G is said to be weighted, if each edge in G is assigned a non-negative numerical value. w (e) = Weight or length of edge e

Multigraph:  If a graph is having multiple edges and/or loops, then it will be called a multigraph.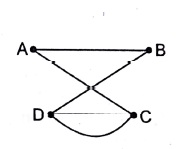

Multiple Edges: Distinct edges e and e’ are called multiple edges, if they connect the same endpoints i.e., if e [u, v] and e’ [u, v].

Loops: An edge e is called a loop, if it has identical stmt point and end. point i.e., if e = [u,  µ].

Directed Graph (Digraph)

Each edge in graph G is assigned a direction or each edge e is identified with an ordered pair (u, v) of nodes G rather than an unordered pair [u, v].

u is predecessor of v and v is a successor of u or neighbour of

u is adjacent to v and v is adjacent to u.

• Outdegree of a node u in G

outdeg (u) = Number of edges beginning at u

• Indegree of a node u in G –

indeg(u) = Number of edges ending at u

• A node u is called source, if it has positive outdegree but zero indegree
• A node u is called sink, if it has a zero outdegree but a positive indegree

 

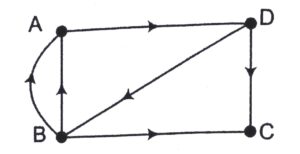
indeg(c) = 2;  outdeg (c) = 0

So, C is a sink and there is no source node of this graph.

Adjacency Matrix

suppose G is a simple directed graph with m nodes and suppose the nodes of G have been  ordered are called v₁,v₂,…,v_m.

Then adjacency matrix (A) = (aij ) of the graph G is the m x m matrix defined as follows

Such a matrix which contains entries of on by 0 and 1, is called a bit matrix or a Boolean Matrix.

The  adjacency matrix A of the graph G does depend on the ordering of the nodes of G; i.e  a different ordering of the nodes may results in a different adjacency matrix.

---

Importance of Turing Machine Tutorial Notes Study Material with Examples

Follow Us on Social Platforms to get Updated : twiter,  facebook, Google Plus

Learn Turing Machine in Handbook Series:  Click here