Compiler Design Tutorial Notes Study Material with Examples

Compiler Design

Compiler

A compiler is a program written in one language (i.e., source language) and translate it into an equivalent program in a target language.

This translation process could also report the errors in the source system, if any.

Major Parts of a Compiler

 There are two major parts of a compiler

1. Analysis                 2. Synthesis

• In analysis phase, an intermediate representation is created from the given source ,” Lexical analyzer, syntax and analyzer and semantic analyzer are phases in this part.
• In synthesis phase, the equivalent target program is created from this Intermediate Intermediate code generator and code optimizer are phases in this part.

Phases of a Compiler

Each phase shown in the figure (phases of a compiler) transform from representation into another representation. They communicate With the error  handlers and the symbol table.

 Lexical Analyzer

Lexical analyzer reads the source program character by character and returns the tokens of the source program. It puts information about  identifiers into the symbol table. Some typical task of lexical analyzer includes recognizing reserved keywords, ignoring comments, binding integer and floating Point constants.

Counting the number of lines, finding identifiers (variables) finding string and character constants, reporting error messages and treating white spaces appropriately in the form of blank, tab and new line characters.

Tokens, Lexemes and Patterns

• A token describe a pattern of characters having same meaning in the source program such as identifiers, operators, keywords, numbers, delimiters and so on, A token may has a single attribute which holds the required information for that token. For identifiers, this attribute is a pointer to the symbol table and the symbol table holds the actual attributes for that token.
• Token type and its attribute uniquely identify a lexeme.
• Regular expressions are widely used to specified pattern.

Note:  A token can represent more than one lexeme, additional information.(Le., attribute of the token) should be held for that specific lexeme.

Specification of Tokens

Regular expressions are an important notation for specifying patterns. Each pattern matches a set of strings, so regular expressions will serve as names for sets of string.

Recognition of Tokens

Lexical analyzer are based on a simple computational model called as the

finite state automata.

Transition diagram depicts the actions that take place when a analyzer is called by the parser to get the next token.

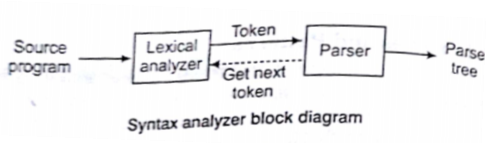
Syntax Analyzer (Parser)

Syntax analyzer creates the syntactic structure of the given source program. This syntactic structure is mostly a parse tree. The syntax of a Program. This is described by a Context-Free Grammar (CFG). We will use BNF (Backus-Naur Form) notation in the description of CFG^.

The syntax analyzer (parser) checks whether a given source program, This  syntactic structure is mostly a parse tree.or not. If it satisfies the parser creates the parse tree of that program. Otherwise the parser given the error message.

Key Points

• A context-free grammar gives a precise syntactic specification of a programming language.
• The design of the grammar is an initial phase of the design of a computer.
• A grammar can be directly converted into a parser by some tools which works on stream of tokens and the smallest item.
• Parser sends get next token command to lexeme to identify next token.

We categorize the parser into two groups

• Top-down parser (starts from the root).
• Bottom–up parser (starts from the leaf).
• Both top-down and bottom-up parser scan the input from left-to right (one symbol at a tine) .
• Efficient top-down and bottom-UP parser can be implemented only for sub-classes of context-free grammars.

(i) LL for   top-down parsing

(ii) LR for bottom-up parsing

Context-Free Grammars

Inherently recursive structures of a programming language are defined by  a CFG. In   a CFG, we have A start symbol (one of the non-terminals).  A finite set of  terminals  (in our case, this will be the set of tokens). A set  of  non-terminals (Syntactic variables).

A finite set of production rules in the following form

A →α ,where  A is non-terminal and α is a string of terminals (including the empty string).

Derivations

It refers to replacing an instance of a non-terminal in a given string’s non terminal by the right hand side of production rule, whose left hand side contains the  non-terminal to be replaced. Derivation produces a new String contained only terminal symbols, then no further.

Derivation is possible

            E=> -E, is read as “E derives –E”.

Each derivation step needs to choose a non-terminal to rewrite and a production rule to apply. A left most derivation always chooses the left most non-terminal to rewrite.

e.g.,    E=> E+E => id + E => id + id

A right most derivation always chooses the right most non-terminal to rewrite.

e.g.,  E=> E + E => E +id => id + id

Parse tree

Graphical representation for a derivation that filters out the order of choosing non-terminals to avoid rewriting. The root node represents the start symbol, inner nodes of a parse tree are non- terminal symbol.

The leaves represent terminal symbols

          E=> -E                                    

• -(E)
• -(E+E)
• -(id + E)
• -(id +id)

Ambiguity

            A grammar produces more than one parse tree for a sentence is called as ambiguous grammar. Unambiguous grammar refers unique selection of the parse tree for a sentence.

We should eliminate the ambiguity in the grammar during the design phase of the compiler. Ambiguous grammars can be disambiguate according to the precedence and associativity rules.

e.g consider the grammar

                        E =>E + E | E+E|id

If we start with the E => E+E, then the parse tree will be created as follows.

If we start with the E => E*E, then parse tree will be created as follows.

Note:  The above grammar is ambiguous as we are getting more than one Parse tree for it_.

Removing Ambiguity

Consider an example of ambiguous grammar as given below

       E →E+EIE*EIE^ElidI (E)

We can use precedence of operators as follows

^ (right to left)
* (left to right)
+ (left to right)

Using the above operator precedence and associativity, we get the following unambiguous grammar

E →E+T|T

T →T*F1F

F → G^FIG

G –> id |(E)

Left Recursion

A grammar is left recursive, if it has a non-terminal A such that there derivation.

          A => A α for some string α

Top-down parsing technique can’t handle left recursive grammars. So, we have to to convert our left recursive grammar into an equivalent grammar which is not left recursive. The left-recursion may appear in a single step of the derivation (immediate Left recursion) or may appear in more than one step of the derivation^.

Left Factoring

A predictive parser (a Top-down parser without backtracking) insists that the grammar must be left factored.

Grammar → a new equivalent grammar suitable for predictive parsing.

Stmt → if expr  then stmt eels stmt | if expr then stmt

When we see, if we can’t know which production rule is to be chosen then rewrite stmt in the derivation.

In general.

                     A → α₁ β₁ | α₂ β₂

Where α is not empty and the first symbols of β₁ and β₂ (if they have one) are different.

When processing α, we can’t know whether expand

              A to α β₁ or

              A to α β₂

But, if we rewrite the grammar as follows

              A → αA¹

                A¹ → α₁ β₁ | α₂ β₂, so we can immediately expand A to αA¹.

YACC

YACC generates C code for a syntax analyzer or parser, YACC uses grammar rules that allow it to analyze token from LEX and create a syntax tree. A syntax tree imposes a hierarchical structure tokens. e.g., operator precedence and associativity are apparent in the syntax tree.

YACC takes a default action when there is a conflict. For shift reduce conflicts, YACC will shift. For shift reduce conflict, it will use the first rule in the listing. It also issues a warning message whenever a conflict exists.

Key Points

• The warning may be suppressed by making the grammar unambiguous.
• The definition S section consists of token declarations and C code bracketed by “%(“and ” %)”.
• The BNF grammar is placed in the rules section and the user subroutines are added in the subroutines section.
• input to YACC is divided into three sections

… definitions …

%%

….rules….

%%

… subroutines …

Top-down Parsing

There are two main techniques to achieve top-down parse tree 0) Recursive descent parsing

(ii) Predictive parsing

• Recursive predictive parsing
• Non^–recursive predictive parsing

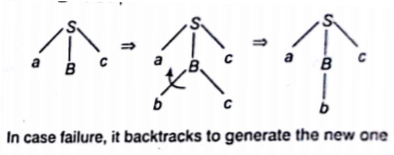
Recursive Descent Parsing (Uses Backtracking)

Backtracking is needed (if a choice of a production rule does not work, we backtrack to try other alternatives). it tries to find the left most  derivation. It is not efficient.

e.g., If the grammar is

                                    S →aBc

                                    B →bc|b and the input is abc

Predictive Parser

Grammar ——————à ——————à  A grammar suitable for predictive

                Eliminate                             Left       

                left recursion                     factor

parsing a LL(1) grammar (no 100% guarantee).

When re-writing a non-terminal in a derivation step, a predictive parser

can uniquely choose a production rule by just looking the current symbol in input string.

e.g.,       stmt   –>  à if —–|       

                               while ——|

                              begin ——-|

                              for——-|

• When we are trying to write the non-terminal stmt, we have to choose first production rule.
• when we are trying to write the non-terminal stmt, we can uniquely choose the production rule by just looking the current token.
• We eliminate the left recursion in the grammar and left factor it. But it may not be suitable for predictive parsing (not LL (1) grammar)

Recursive Predictive Parsing

Each non-terminal corresponds to a Procedure

e.g.,    Aà –> aBb / bAB

Proc A

{

          case of the current token

            {

          ‘a’ – match the current token with a and move to the next token;

                   -call B;

                        -match the current token with and move to the next token;

            ‘b’ -match the current token with b and move to the next token;

                   -cal l ‘A’ ;

                   – cal l ‘B’

Non-recursive Predictive Parsing (LL (1) Parser)

Non-recursive predictive parsing is a table driven parser.

It is a top-down parser.                • It is also known as LL (1) parser.

Input buffer:  Our string to be parsed. We will assume that its en is marked with a special Symbol $.

Output:  A production rule representing a step of the derivation sequence (left most derive ion) of the string in the input buffer.

Stack:  Contains the grammar symbol. At the bottom of the stack, there is a special end marker symbol $. Initially the stack contains only the symbol $ and the starting symbol S ($S initial stack). When the stack is emptied (i.e., only $ left in the stack), the parsing is completed.

Parsing table

• A two-dimensional array M [A, a].
• Each row is a non-terminal symbol.
• Each column is a terminal symbol or the special symbol $.
• Each entry holds a production rule.

Parser Actions

The symbol at the top of the stack (say X) and the current symbol in the  input string (say a) determine the parser action.

There are four possible parser actions

1. If X and a are S -4 parser halts (successful completion).
2. If X and a are the same terminal symbol (different from S’). Parser pops X from the stack and moves the next symbol in the input buffer.
3. If X is a non-terminal.

Parser looks at the parsing table entry M [X, a]. If M[X, a] hold a production rule X –> Y₁, y₂.,., Y_k, it pops X from the stack and  pushes Y_K,Y_k-1 , ……, Y₁ into stack. The parser also outputs the production rule –>Y₁, y₂.,., Y_k, tp re[resent a step of the derivation.

 (iv) None of the above–> error

All empty entries in the parsing table are errors. If X is a terminal symbol different from a, this is also an error case .

Functions used in Constructing LL (1) Parsing Tables

• Two functions are used in the construction of LL (1) Parsing Tables-FIRST and FOLLOW.
• FIRST (α) is a set of the terminal symbol strings derived from a, where α is any string of grammar symbols It α derives to ϵ. then ϵ is also in FIRST (α).
• FOLLOW (A) is the set of the terminals which occur immediately (FOLLOW) the non^–terminal A in the strings derived from the starting
• A terminal a is in FOLLOW (A), if S => aAa β.
• $ is in FOLLOW (A)_; if S => αA

To Compute FIRST of any Strings X

• if Xa terminal symbol –>FIRST (X)={X)
• If X is a non-terminal symbol and X –>Ɛ is a production rule–> Ɛ is in FIRST (X).
• If X is a non-terminal symbol and X –>Y₁, Y₂….Y_n is a production rule
  if a terminal a in FIRST (Y₁) and ϵ is in all FIRST (Y_j) for j=1,…., i-1 then a is in FIRST (x).

If Ɛ is in all FIRST (Y_j) for j =1,….n then ϵ is in FIRST (X).

• If X is c, Then FIRST (X) = { ϵ}
• If X iS If X iS Y_1, Y_2,….Y_n

If a terminal a in FIRST (Y,) and ϵ is in all FIRST (Y_j) for j=1 … r -1 then  a is in FIRST (X). If ϵ is in all FIRST (Y_j) for j=1,….n then ϵ is in FIRST (X).

To compute FOLLOW (for Non^–terminals) .If S is the start symbol, $ is in FOLLOW (S).

• if A–>Bβ is a production rule, then everything in FIRST (β) is FOLLOW(B) except ϵ.
• If (A ->aB is a production rule) or (A –4aBl3 is a production rule and !s n FIRST (V then everything in FOLLOW (A) is in FOLLOW (B).
• Apply these rules until nothing more can be added to any FOLLOW set.

Bottom-up Parsing Techniques

A bottom-up parser creates the parse tree of the given input string from leaves towards the root. A bottom-up parser tries to find the right most .derivation of the given input in the reverse order.

(I)  S           =>       –  – – => ω (the right most derivation of ω).

(ii)         ←       (the bottom-up parser finds the right most derivation in the

reverse order).

Bottom-up parsing is also known as shift reduce parsing.

Shift Reduce Parsing

A shift reduce parser tries to reduce the given input string into the starting symbol. At each reduction step, a substring of the input matching to the right side of a production rule is replaced by the non-terminal at the left side of that production rule.

Note: If the substring is chosen correctly, the right most derivation of that string is created in the reverse order.

Handle

Informally, a handle of a string is a substring that matches the right side of a Production rule, but not every substring that matches the right side of a Production rule is handle, A handle of a right sentential form y (Ξαβω) is a Production rule A–>β  and a position of y, where the string β may be found and replaced by A to produce the previous right sentential form in a right most derivation of y.

S => aAω => aβω, where co is a string of terminals.

If the grammar is unambiguous. Then every right sentential form of the grammar has exactly one handle. A right most derivation in reverse can be obtained by Handle-pruning.

Stack Implementation

There are four possible actions of a shift reduce parser.

• Shift The next input symbol is shifted onto fop of the stack.
• Reduce Replace the handle on the top of click by the non-terminal.
• Accept Successful completion of parsing.
• Error Parser discover a syntax error and calls an error recovery routine.
• Initial stack just contains only the end-marker $.
• The end of the input string is marked by the end-marker $.

Conflicts During Shift Reduce Parsing

There are CFCs for which shift reduce parser can’t be used. Stack center. Stack contents and the next input symbol may not decide action.

Shift/Reduce Conflict

Whether make a shift operation or a reduction.

Reduce/Reduce Conflict

The parser can’t decide which of several reductions to make.

• If a shift reduce parser can’t be used for a grammar, that grammar called as non-LA (k) grammar.
• An ambiguous grammar can never be a LR grammar.

 

Types of Shift Reduce Parsing

There are  two main categories of shift reduce parser.

Operator Precedence Parser

Simple, but supports Only a small class of grammars.

LR Parser

Covers wide range of grammars

• SLR Simple LR parser
• CLR Most general LR parser (canonical LR)
• LALR Intermediate LR parser (look-ahead LR)

SLR. CLR and LALR work in same way. but their parsing tables are different

Operator grammar small but an important class of grammars. We may have an efficient operator precedence parser (a shift reduce parser) for an operator  grammar.

In operator grammar, no production rule can have ϵ at the right side and adjacent non-terminals at the right side.

Precedence Relations

In operator precedence parsing, we define three disjoint precedence relations between certain pair of terminals.

a < b, b has higher precedence than a.

a = b, b has same precedence as a.

a > b, b has lower precedence than a.

The determination of correct precedence relation between terminals are based on the traditional notions of associativity and precedence of operators.

• Scan the string from left end until the first > is encountered.
• Then, scan the backwards (to the left) ove.
• Using precedence relations to find handler any ‘=’ until a ‘<’ is
• The handle contains everything to the first ‘>’ and to the right of the ‘ is

The handles thus obtained can be used to shift reduce a given string.

 Handling Unary Minus

• Operator precedence parsing can’t handle the unary minus, when we also use the binary minus in our grammar
• The best approach to solve this problem is to let the lexical analyzer handle this problem, as the lexical analyzer will return two different operators for the unary minus and the binary minus.
• Lexical analyzer will need a look-head to distinguish the binary minus form the unary minus.

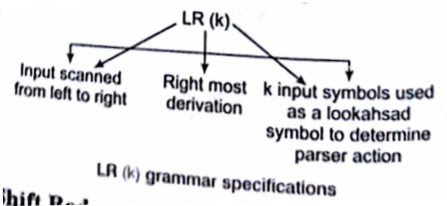
LR parsing

LR parsing is most general non-back tracking shift reduce parsing. The class of grammars that can be parsed using LR methods is a proper superset of the class of grammars that can be parsed with predictive parser.

LL (1) grammars  (c LR (1) grammars

An LR parser can detect a syntactic error as soon as it is possible^.

A configuration of a LR parsing is

      (S₀ X₁ S₁……….X_mS_m , a_;a_{; i}_ …a_n $)

            Sta^,ck    Rest of input

• S_m and a, decides Tl^– parser action by consulting the parsing action to (initial stack contains just S_o).
• A configuration of a 1.1R parsing represents the right sequential form

                X₁… X_m a₁ a_;+1..•a_n$

LR Parser Actions

Shift S Shift the next input symbol and the state S onto the stack

(S₀ X S₁…. X_m S,a,a_i+1…a_n$) –>

                                                (S₀ X S₁…. X_m S_m,a_is,a_i+1…a_n$)

Reduce A –>β (or , where n is a production number)

Pop 2|β|(=r) items from the stack; let us assume that β=Y_1, Y₂ …… Y_r.

 Then, push A and S. where S , goto [S_m-r,A]

   (S₀ X S₁…. X_m S,a,a_i+1…a_n$) –>

                                                (S₀ X S₁…. X_m-r S_m-r ,As,a_i…a_n$)

Accept:  parsing successfully completed.

Error:  parser detected an error (an empty entry in the action table).

---

Sorting in Design and Analysis of Algorithm Study Notes with Example

Learn Sorting in Handbook Series:  Click here 

Follow Us on Social Platforms to get Updated : twiter,  facebook, Google Plus