Binary Codes Tutorial with Examples in Switching Theory and Computer

Binary Codes

Binary codes are codes which are represented in binary system with modification from original ones.

Weighted Binary System

Weighted binary codes are those which obey the positional weighting principles, each position of a number represents a specific weight.

e.g.,   8421,  2421,   5211.

Sequential Code

A code is said to be sequential when two subsequent codes, seen as numbers in binary representation, differ by one. The 8421 and excess-3 codes are sequential, whereas 2421 and 5211 codes are not.

Non-weighted Codes

Non-weighted codes are codes that are not positionally weighted. That is  each position within the binary number is not assigned a fixed value.

Reflective Code 

A code is said to be reflective when code for 9 is complement for the code for 0 and so is for 8 and 1 codes, 7 and 2, 6 and 3, 5 and 4. Codes 2421, 5211 and excess-3 are reflective, whereas the 8421 code is not.

BCD (Binary Coded Decimal)

it is a straight assignment of the binary equivalent. To encode a decimal number using the common BCD encoding. Each decimal digit is stored in  a 4-bit number.

BCD encoding for number 127 would be

                          1           2             7

(0001 0010 0111)–> BCD equivalent of 127 whereas the pure binary number would be (01111111)₂

BCD Addition

Add (148 + 157) =?

When sum of 2 digits is greater than or equal to 9, then we need to add 6 i.e., 0110.

2421 Code

^This is a weighted code, its weights are 2,4,2 and 1. A decimal number is ^represented in 4 bit form and the total 4 bits weight is

2 + 4 + 2 + 1= 9.

Hence, 2421 code represents the decimal numbers from 0 to 9.

Excess-3 Code

Excess- 3 is a non-weighted code used to represent decimal numbers. The code derive its name from the fact that each binary code is the corresponding 8421 code plus 0011(3).

e.g.,                                      Decimal                   8421                                            Excess – 3

8                          1000                              1000+0011-1011

6                           0110                              0110+0011 1001

---

Gray Code

This is a variable weighted code and is cyclic. This means that it is arranged, so that every transition from one value to the next value involves only one bit change.

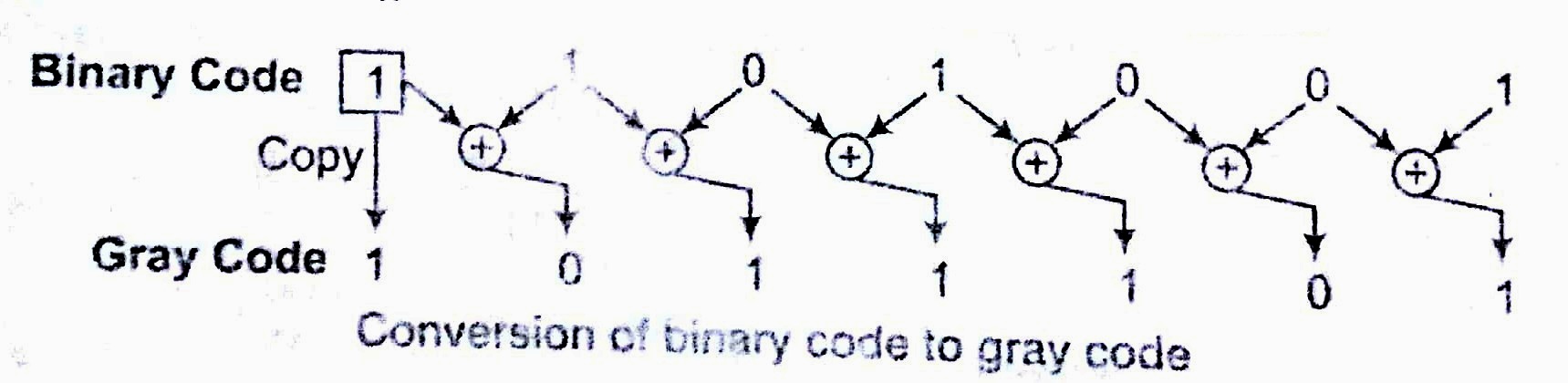
Binary to Gray Code Conversion

1. Write down the  number in binary codes.
2. The Most Significant Bit (MSB) of the ^.gray code will be same as the MSB of binary coo
3. Perform XOR operation on MSB and next bit to the MSB in binary number.
4.  Repeat step 3 till all bits of binary number have been XOR operation, the resultant code ;s: the  gray code equivalent to binary code.

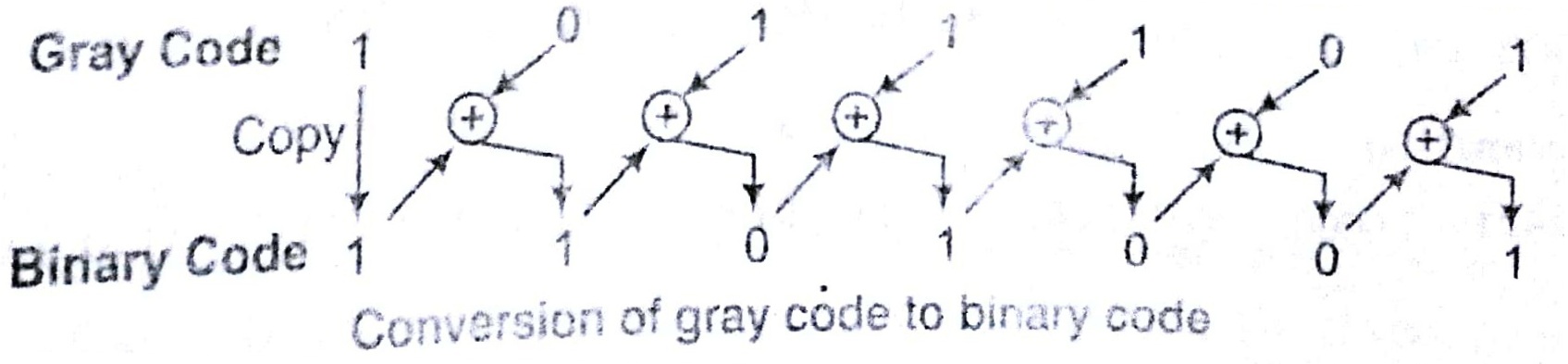
Gray Code to Binary Conversion

     1. Start with the MSB of gray/ coded =number.

2. Copy this bit as the MSB of the binary number.
3. Now^., perform Ex-OR operation of this bit with the next bit of the binary number. 
4. Repeat step 3 till all bits of gray coded number have been used in XOR operation. The resultant number is the binary equivalent of the gray number.

5. 

---

Sorting in Design and Analysis of Algorithm Study Notes with Example

Follow Us On Cyber Point Solution Youtube Channel : Click Here

Follow Us on Social Platforms to get Updated : twiter,  facebook, Google Plus

Learn More Ethical Hacking and Cyber Security click on this link. cyber security