A Short Course Compiler Grammar Tutorial Study Notes with Examples
What is Compiler Grammar
In 1956, Noam Chomsky gave a model of grammar. A grammar is defined as 4-tuples (VN, Ʃ, P, S),
Where, VN is finite non-empty set of non-terminals.
Ʃ is finite non-empty set of input terminals.
P is finite set of product rules.
S is the start symbol.
What is Chomsky Hierarchy
The Chomsky hierarchy is a containment hierarchy of classes of formal grammars that generate formal languages. The formal grammars consist of a finite set of terminal symbols, a finite set of non-terminal symbols, a set of production rules with a left and a right hand side consisting of a word of these symbols and a start symbol.
The Chomsky hierarchy consists of following four levels.
Type 0 Grammar (Unrestricted Grammar)
These are unrestricted grammars which include all formal grammars. These grammars generate exactly all language that can be recognized by a Turing machine.
Rules are of the form α → β.
Where, α and β are arbitrary strings over a vocabulary V and α ≠ ^ (null).
Type 1 Grammar (Context Sensitive Grammar)
Language defined by type-1 grammars are accepted by linear bounded automata.
Rules are of the form α A β → α B β
Where, A ϵ VN
α , β, B ϵ (VN U Ʃ)
B ≠ ^
Type 2 Grammar (Context-free Grammar)
Language defined by type-2 grammars are accepted by push-down automata.
Rules are of the form A → α
Where, A ϵ VN
α ϵ (VN U Ʃ)*
Type 3 Grammar (Regular Grammar)
Language defined by type-3 grammars are accepted by finite state automata.
Rules are of the form A → ^
A → α
A → α β
Where, A, B ϵ VN and a ϵ Ʃ

Regular Expression
Regular expression mean to represent certain sets of strings in some algebraic fashion.
A regular expression over the alphabet E is defined as follows
- ɸ is a regular expression corresponding to the empty language ɸ.
- ^ is a regular expression corresponding to the language { ^}.
- For each symbol a ϵ E, a is a regular expression corresponding to the language {a}.
Regular Language
The Language accepted by FA are regular language and these language are easily described by simple expressions called regular expressions.
For any regular expression r and s over E, Corresponding to the language Lr and LS respectively, each of the following is a regular expression corresponding to the language indicated.
- (r s) corresponding to the language Lr L
- (r + S) corresponding to the language Lr U L
- r* corresponding to the language Lr.
Some examples of regular expression are
L (01) = {0,1}
L (01 +0) = {01,0}
L(0(1+0))={01,00}
L(0*) = {Ɛ, 0, 00, 000, …..}
L((0 +10)* (^ + 1) = all string of 0’s and 1’s without two consecutive 1’s.
Key Points
- If L1 and L2 are regular language in E* , then L1 U L2, L1 ∩ L2, L1 – L2 and L1’ (complement of L1 ), are all regular languages.
- Pumping lemma is a useful tool to prove that a certain language is not regular.
- The Myhill-Nerode theorem tells that the given language might be regular or not regular.
Regular Set
A set represented by a regular expression is called regular set.
E.g. If Ʃ = {a, b} is an alphabet, then
Different Regular Sets and their Expressions
| Sets | Regular Expression |
| {} | ɸ |
| {a} | a |
| {a ,b} | a+b |
| { ɛ, a, aa, aaa,….} | a* |
| {a, aa, aaa,….} | aa* = a+ |
Identities for Regular Expressions
The following points are the some identities for regular expressions.
ɸ + L = L + ɸ = L ɸ L = L ɸ = ɸ
^R = R^ = R ^* = ^ and ɸ* = Ɛ
R+ R = R, where R is the regular expression RR* = R*R = R*
(R*)* = R* R*R* = R*
(P + Q)* = (P*Q*)* (P* + Q*)*, where P and Q are regular expressions.
R (P + Q) = RP + RQ and (P + Q) R = PR + QR
R (P + Q) = RP + RQ and (P + Q) R = PR + QR
P (QP)* = (PQ)*P
Regular Expression and Finite Automata
NFA with ^-moves Let r1 and r2 be the two regular expressions over Ʃ1 Ʃ2 and E1 E2 are two NFA for r1 and r2 respectively.
Regular Expression to ^-NFA (union)
For E1 U E2

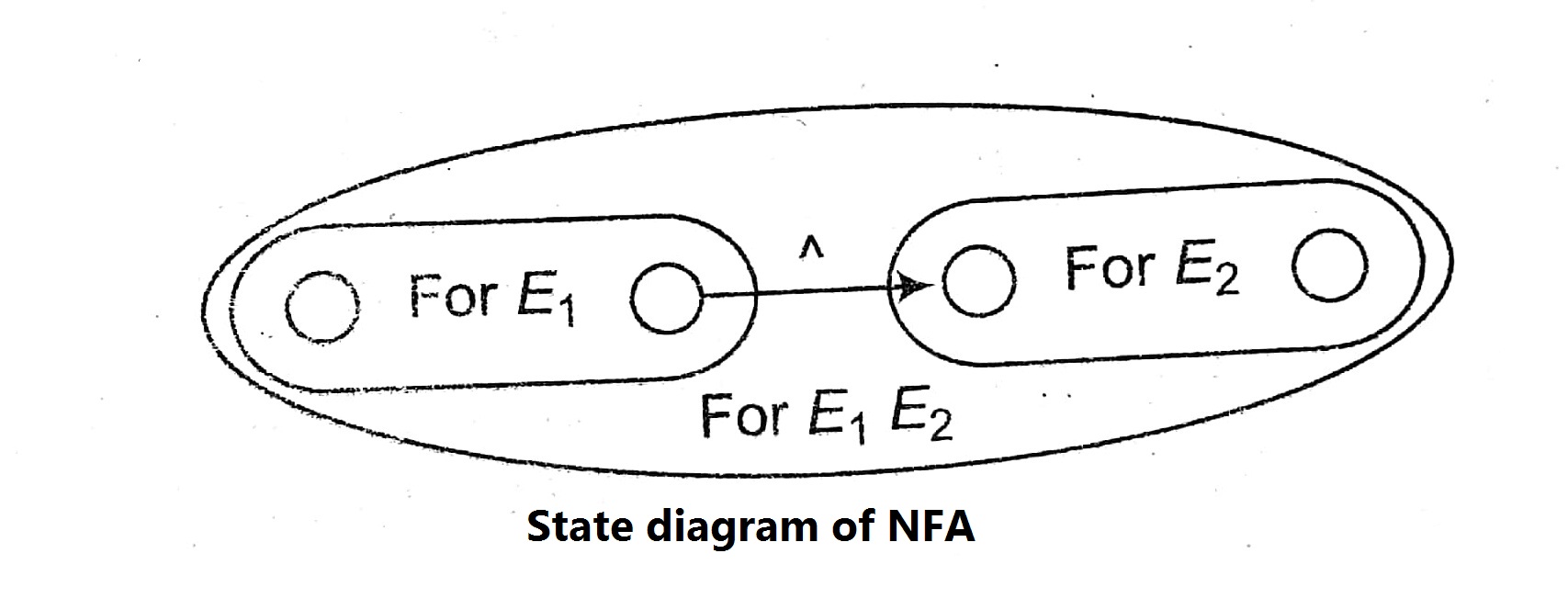
Regular Expression to ^-NFA (Concatenation)
For E1 E2
Regular Expression to ^-NFA (Clousre)
For E*

Construction of Regular Expression from DFA
If a DFA recognizes the regular language L1 then there exists regular expression, which describes L.
Arden’s Theorem
- If P and Q are two expressions over an alphabet Ʃ such that P does not contain ^, then the following equation R = Q + RP.
- The above equation has a unique solution i.e. , R=QP*. Arden’s theorem is used to determine the regular expression represented diagrams.
The following points are assumed regarding position diagrams.
- The transition system does not have any ^.
- It has only one initial (starting) state.
Properties of Regular Languages
Regular Language are closed under following properties.
- Union
- Concatenation
- Kleene closure
- Complementation
- Transpose
- Intersection
- If A is polynomial time reducible to B (i.e., A ≤ B) and B is in P, then Also in P.
- If A is NP-complete problem, then it is member of P if and only if P = NP.
- The complexity class NP-complete is the intersection of NP and NP-hard classes.
Key Points
- All NP problems can be solved, if an NP problem can be reduced to an NP- hard problem before solving it in polynomial time.
- If A is NP- complete and there is a polynomial time reduction of A to B, then B is NP-complete.
- If there is a language L such that L ϵ P, then complement of L is also in P.
- P complexity class is closed under union, intersection, complementation, kleene closure and concatenation.
- NP complexity class is closed under union, intersection, concatenation, and Kleene closure.
Design of Automaton
The design can be illustrated by under following three categories
Sequence of string is fixed
If the sequence of string is fixed that suppose an automaton is designed to accepted a string with abbacb.

The value of string is changed by changing input value
Suppose, an automaton is designed to accepted the string abba or bbba.


When input values are repeated
Suppose an automaton is to be designed for accepting all string generated by input a. That means it has to accept a, aa, aaa, ……
This will be designed as


Now, if we have to design a machine which accepts all inputs containing string ab

Context Free Language Tutorial Notes Study Material with Examples
Follow Us on Social Platforms to get Updated : twiter, facebook, Google Plus
Learn Context Free Language in Handbook Series: Click here
